Algorithms Shortest Path
Data Source: Stadt Wien – data.wien.gv.at
Shortest Path (Point to Point)
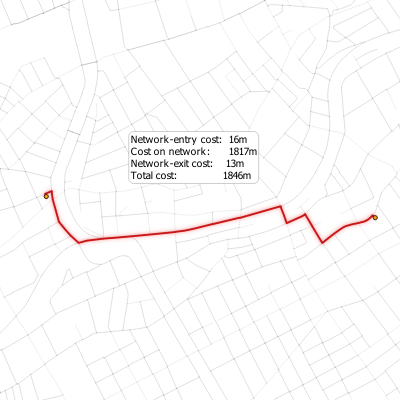
This algorithms is based on the standard Processing Network analysis algorithm (same name) by Alexander Bruy. The special feature of the QNEAT3 implementation is that it uses the concept of off-network travel which is made possible by using the Qneat3AnalysisPoint class. The geometry of the path is not limited to on-network travel but includes the first leg (entry leg) and last leg (exit leg) between the start and endpoints and their respective counterparts on the network
| # | Mandatory Parameters | Type | Info |
|---|---|---|---|
| 1 | Network Layer | Vector Layer | Geometry type must be LineString |
| 2 | Start point (x, y) | Coordinate pair | obtain by clicking on map canvas |
| 3 | End point (x, y) | Coordinate pair | obtain by clicking on map canvas |
| 4 | Optimization Criterion | Shortest | Fastest | - |
| 5 | Shortest Path Layer | Output Vector Layer | - |
| # | Optional Parameters | Type | Info |
|---|---|---|---|
| 1 | Direction field | Field containing direction values | - |
| 2 | Value for forward direction | user input | input must be referenced to Direction field |
| 3 | Value for backward direction | user input | input must be referenced to Direction field |
| 4 | Value for both directions | user input | input must be referenced to Direction field |
| 5 | Default direction | Both Directions | Forward Direction | Backward Direction | |
| 6 | Speed Field | Field containing speed values | must be numerical |
| 7 | Default speed | user input | (!) sets network entry- and exit-speed |
| 8 | Topology tolerance | user input | Tolerate gaps in network (crs units) |